Relating abstract theory to everyday object is a rewarding and illuminating experience. It helps me to develop a deeper understanding of the theory, and a new look on everyday objects. Looking at mattress flipping in the lens of group theory is one of such examples in my recent experience.

Imagine we have a king mattress. Let’s mark its four corners as 1, 2, 3, 4. We can easily see that the mattress can only have the following 4 configurations by rotation and flipping:

Mattress Config

The actions to get from one configuration to another have to be one of these three options: 180-degree rotation, horizontal flip, or vertical flip. Let’s note them as R, HF, and VF, respectively, and add them to the graph:

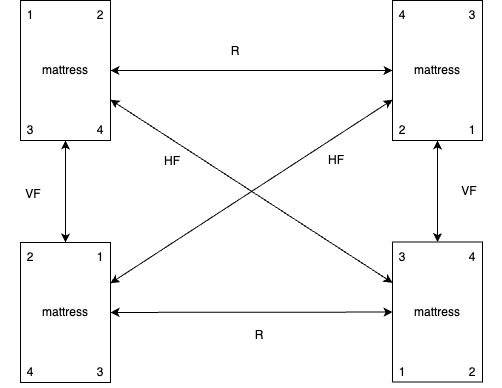
Mattress Config

This is a group! What it means is that if we take these three actions plus an identity element (noted as I, which we can define as no action taken in this case, so four actions in total), it has the following properties:

  • Closed: Any combination of I, R, HF, VF ends up being equivalent to taking one of the four actions. For example, R * VF = HF, HF * R = VF, R * HF * R * VF = R. We can easily verify this by looking at the graph above, and it applies to all the configurations.
  • Associativity: The grouping of a sequence of actions doesn’t affect the result. For example, R * (VF * R) = R * HF = HF * R = (R * VF) * R.
  • Inverse element: Each action has an inverse element such that the combination of their effects is the identity element. In this case, each action is its own inverse (thus the bidirectional arrow in the graph).

A set of elements satisfying such properties is what’s called a group. Furthermore, to clearly see the result of an arbitrary chain of actions, we can use what’s called a Cayley diagram, and the Cayley diagram for mattress flipping is:

  I R HF VF
I I R HF VF
R R I VF HF
HF HF VF I R
VF VF HF R I

Using this diagram, we can easily compute the result of an arbitrary action sequence. We can write some simple code for it:

caylay_diagram = {
    "I_I": "I",
    "I_R": "R",
    "I_HF": "HF",
    "I_VF": "VF",
    "R_I": "R",
    "R_R": "I",
    "R_HF": "VF",
    "R_VF": "HF",
    "HF_I": "HF",
    "HF_R": "VF",
    "HF_HF": "I",
    "HF_VF": "R",
    "VF_I": "VF",
    "VF_R": "HF",
    "VF_HF": "R",
    "VF_VF": "I"
}
def get_result_action(action_seq: str):
    # Assume action_seq is in the format R_R_HF_VF_I_...
    actions = action_seq.split("_")
    result_action = actions[0]
    for action in actions[1:]:
        result_action = caylay_diagram[result_action + "_" + action]
    return result_action

Using the lens of group theory, now we have a deeper appreciation of different ways of flipping a mattress:

  • We know that no matter how we rotate or flip the mattress, we’ll always arrive at one of the four configurations of the mattress (only four configurations without breaking its symmetry).
  • We can easily compute or predict which configuration we’ll arrive at even if we rotate and flip arbitrarily for a long time.
  • We know the least amount of action we should take to go from one configuration to another configuration. For example, we can simply do a horizontal flip instead of a vertical flip plus rotation.